Chapter 10 : Circles - Summary
1. A circle is the collection of all points in a plane, which are equidistant from a fixed point in the plane.
fixed point = centre of the circle
distance of all the points from centre = radius

2. Equal chords of a circle (or of congruent circles) subtend equal angles at the centre.
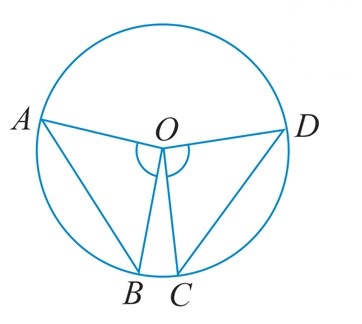
Here - Angle AOB = Angle COD ( if AB = CD => chords are equal)
Hint for proof - Prove that both the triangles AOB and COD are congruent using SSS rule of congruence.
3. If the angles subtended by two chords of a circle (or of congruent circles) at the centre (corresponding centres) are equal, the chords are equal.
[Inverse of the theorem mentioned in Point 2]
4. The perpendicular from the centre of a circle to a chord bisects the chord.

AB = a given chord
AX = BX
OX is perpendicular to AB.
angle OXA = OXB = 90 degree [Given]
Hint for proof :- Prove that triangle OXA and OXB are congruent. (Using RHS rule of congruence)
5. The line drawn through the centre of a circle to bisect a chord is perpendicular to the chord. [ Inverse of the theorem given in Point-4 ]

if OX = line segment drawn from centre of the circle to chord
and AX = BX [ OX bisects the chord AB ]
then OX is perpendicular to AB.
6. There is one and only one circle passing through three non-collinear points.
7. Equal chords of a circle (or of congruent circles) are equidistant from the centre (or corresponding centres).
8. Chords equidistant from the centre (or corresponding centres) of a circle (or of congruent circles) are equal.
9. If two arcs of a circle are congruent, then their corresponding chords are equal and conversely if two chords of a circle are equal, then their corresponding arcs (minor, major)
are congruent.
10. Congruent arcs of a circle subtend equal angles at the centre.
11. The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
12. Angles in the same segment of a circle are equal.
13. Angle in a semicircle is a right angle.
14. If a line segment joining two points subtends equal angles at two other points lying on the same side of the line containing the line segment, the four points lie on a circle.
15. The sum of either pair of opposite angles of a cyclic quadrilateral is 1800.
16. If sum of a pair of opposite angles of a quadrilateral is 1800, the quadrilateral is cyclic.